node-red-contrib-quantum 0.4.0

Quantum computing functionality for Node-RED

npm install node-red-contrib-quantum

node-red-quantum

Node-RED Quantum provides a set of nodes to build and run quantum computing algorithms within Node-RED.

Please be aware that this is a development version of Node-RED Quantum, it is still a work in progress and the code is unstable.

The aim of this module is to help introduce users to quantum computing by providing a library of highly documented nodes for building and running quantum circuits in Node-RED. It was designed to facilitate the integration of quantum algorithms within classical programs, and allows for scalability by providing the fundamental quantum circuit building blocks.

For detailed documentation on how to use each node, please head to the Node-RED Quantum wiki.

For the latest changes, please read the CHANGELOG.

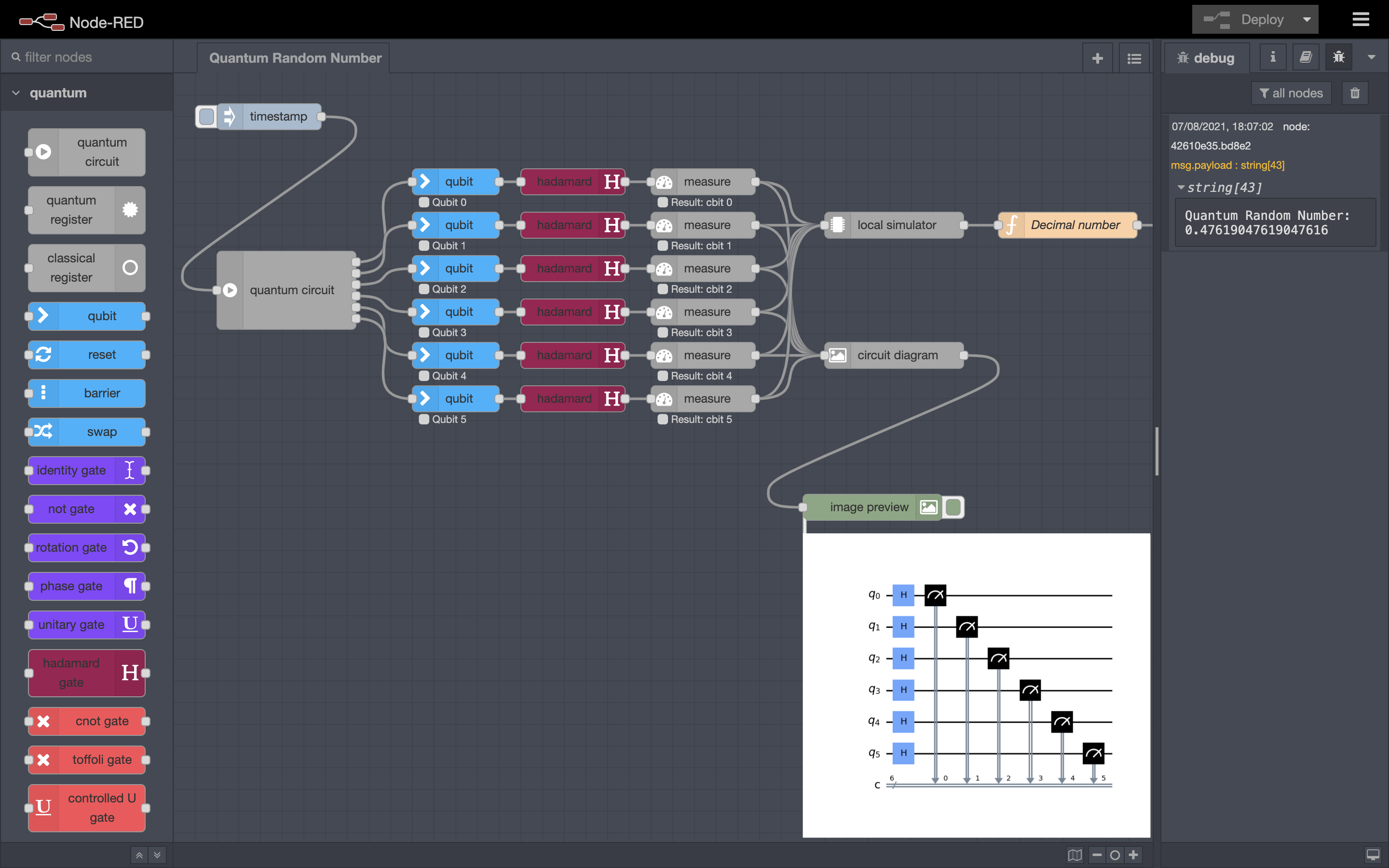
Table of Contents

• Prerequisites
• Installation
  • Docker Alternative
• About Quantum Computing
  • Qubit State
  • Qubit Measurement
  • Entanglement
• Quantum Nodes
  • How to Use
  • Rules
• Quantum Algorithm Nodes
• Contributing
• Acknowledgements

Prerequisites

Node-RED Quantum requires at minimum Node.js 12.0.0, Node-RED 1.0, and Python 3. It is also advised that you start Node-RED from a Bash shell, as it is required to prepare the Python virtual environment.

Even though not required, some knowledge on how to use the Node-RED platfom can be useful. We recommend this Node-RED tutorial on YouTube.

Installation

1. Install Node-RED locally by following the installation instructions here.
2. Once Node-RED has been installed, start the application by entering the command node-red in the terminal.
3. Open the Node-RED interface by navigating to the IP address the server is running at in your browser. This will usually be http://127.0.0.1:1880/.
4. In Node-RED, navigate to the Palette Manager (top-right corner), select Install and search for 'quantum', as depicted below.
5. Install the node-red-contrib-quantum package. Once installed, the quantum nodes provided by this library will show in the Palette (on the left-side of the Node-RED editor). Please note that this installation may take a few minutes, as it needs to install the Python virtual environment required for executing the nodes.

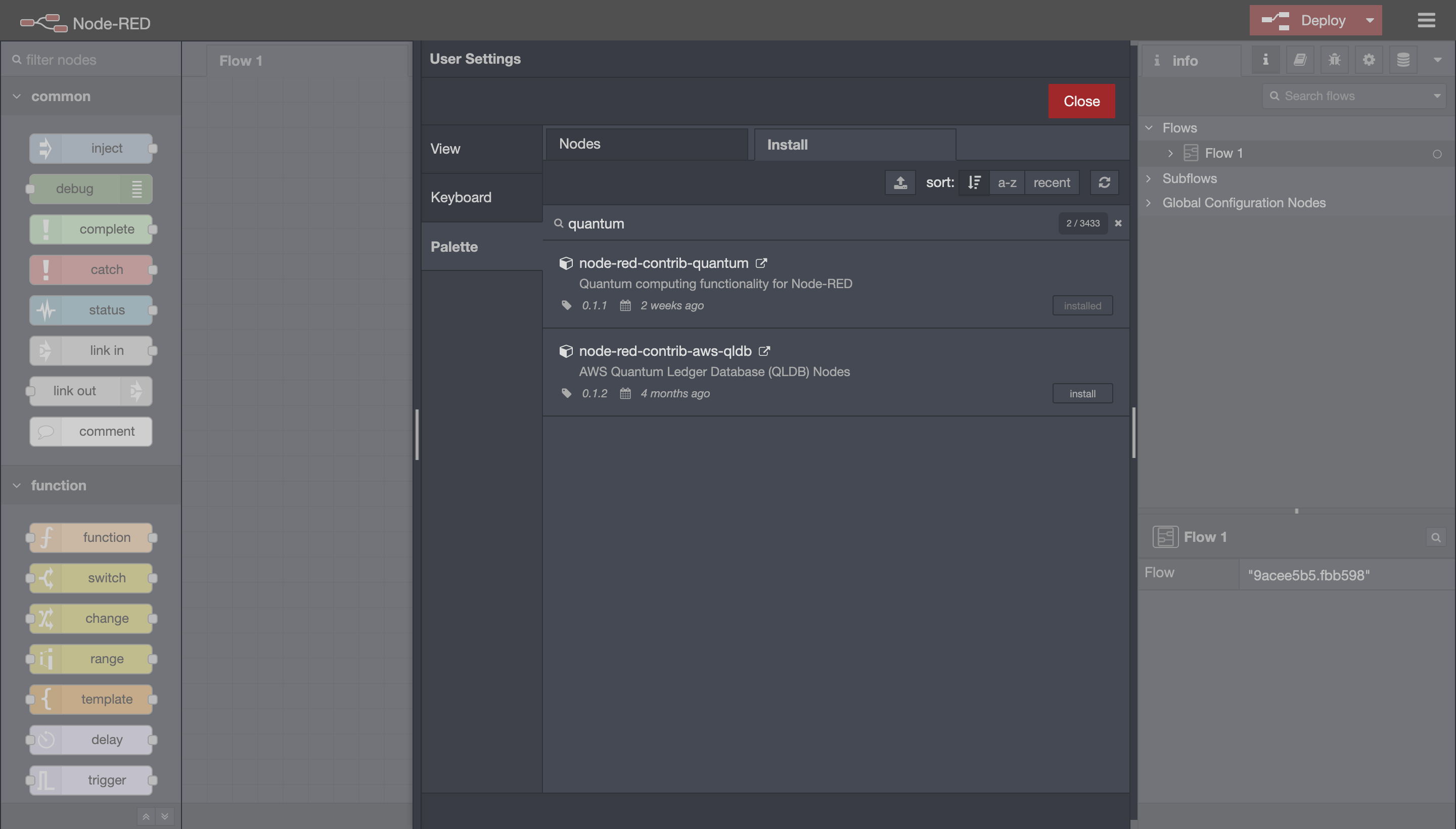
Docker Alternative

An alternative method of installation is to set up a Docker environment:

1. Install docker and docker-compose. The installation guide can be found on the official Docker website.
2. Run docker-compose -p quantum up to start the development container. You can also add -d option to run it in detached mode.
3. If you only need the pre-configured Node.js and Python environment and to install the library on Node-RED interface, run docker build -f Dockerfile.prod -t docker-quantum . to build the image and then run docker run -it -p [local-machine-port]:1880 docker-quantum to start the container. Replace the [local-machine-port] with the desired port that you wish to run Node-RED on your local machine.

About Quantum Computing

Qubit State

A qubit is the same to a quantum computer as what a bit is to a classical computer: the smallest unit of information.

The Bloch sphere representation is considered the most simple and ludic way to understand & visualise a qubit (see example below). In contrast with classical bits that can only be in a '0' or a '1' state, qubits can store much more information. In fact, all points on the sphere represent a different qubit state, the usual classical bit states being labelled as:

• State 0
• State 1

Quantum states that are in between those 2 points are a weighted combination of the '0' and '1' states. This is called superposition. To set the qubit in a particular state, we operate rotations or reflections of the Bloch sphere while keeping the x, y and z axis unchanged.

The Qiskit textbook provides more information on classical vs quantum bits, as well as bloch spheres.

Example:

Applying a π radians rotation about the x-axis on a qubit that is in the '0 state' will put it in the '1 state'.

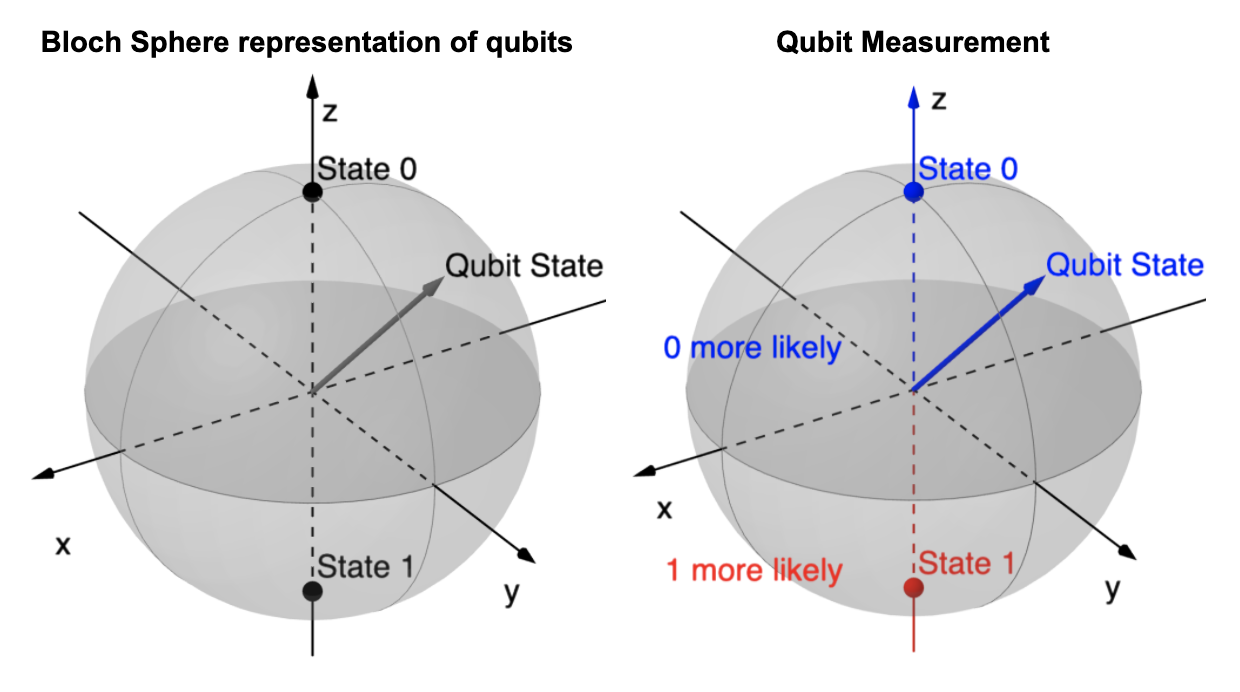
Qubit Measurement

It is very important to understand that even though a qubit can take an infinite number of states, modern technology only allows us to measure '0' or '1', same as a classical bit. Since we measure and interpret a qubit state using classical machines, this can be seen as a projection of quantum computing back to classical computing: from quantum states back to binary values.

This leads to probabilistic measurement results. In terms of the Bloch Sphere, the closest the qubit state is from the '1' state, the more likely we are to measure a '1'.

The act of measuring a qubit collapses the qubit state; the state of the qubit after being measured is not representative of the qubit state before the measurement. You must be careful to ensure that measurement of the qubits happens at the end of the quantum circuit, or reset them after a measurement.

More information on qubit measurement can be found in the Qiskit Textbook

Example:

If we measure a qubit that has a state in the x-y plane 1000 times, then we will approximately get 500 '0' measurements and 500 '1' measurements.

Entanglement

Referred to as a "spooky action at a distance" by Albert Einstein, entanglement is a quantum phenomenon that is extremely powerful in quantum computing; it is a form of connection that can exist between any number of qubits. Here we will illustrate entanglement between two qubits.

Two qubits are said to be entangled when their relative states rely on each other. In other words, changing or knowing the state of one qubit can change the state of the other qubit. This connection is independent of time and space: the two qubits can be miles appart and the connection will still be instantaneous.

In practice, entanglement arises when the operation of a gate on a qubit is conditional on the state of another qubit (similar to an if block in classical computing). These gates are often referred to as multi-qubits quantum gates.

More information on entanglement can be found in the Qiskit Textbook

Example:

A CNOT gate applies a NOT gate (0 → 1 & 1 → 0) to the 'target' qubit if and only if the 'control' qubit is in the '1' state.

Now, let's assume that the 'control' qubit is in a superposition state (25% '0' / 75% '1'), while the 'target' qubit is in the '0' state. Then, the combined state of the 2 qubits after applying the CNOT gate will be:

• '00' with 25% probability
• '11' with 75% probability, (NOT gate applied)

The 2 qubits are now entangled: if we measure one of them to be in a specific state, then we know the other one will be in the same state.

Quantum Nodes

Node-RED Quantum includes a 'quantum' library of nodes that can be used to build quantum circuits.

How to Use

The 'Quantum Circuit' node can generate a quantum circuit with qubits. The qubits will then flow through a certain set of nodes corresponding to quantum operations, or gates. Finally, all qubits must be connected to a single output node that will process the circuit and output the results.

The nodes are organised into 4 categories:

• Input nodes (gray) are used to set up a quantum circuit and output qubits. To start, use the 'Quantum Circuit' node to generate one qubit through each output.

• Qubit nodes (blue) are used to keep track and manage qubits, such as resetting them. The 'Qubit' node receives qubits as input but does not execute any operation on it. It can be used to identify qubits, by printing some text under the node, or to rearrange the position of qubits into the editor.

• Quantum Gate nodes correspond to quantum operations. When a qubit flow through a quantum gate node, the operation is executed on the qubit. There are 2 type of quantum gates:

  • Singe qubit gates (purple) receive a qubit, execute an operation, and output the qubit. The 'NOT Gate' flips the state of the qubit (0 → 1 & 1 → 0).
  • Multi qubits gates (red) receive a certain number of qubits, execute a control operation and output the qubits. Control operations correspond to the conditional execution of a single quantum gate. If the 'control' qubits are in the correct state, then the gate is applied on a 'target' qubit. The 'CNOT Gate', operating on 2 qubits, applies a NOT gate on the 'target' qubit if the 'control' qubit is in the '1' state.

• Output nodes (grey) are used to process the quantum circuit and generate an output. All qubits of the quantum circuit must be connected to the same output node for it to work. The output format varies between each node, please refer to the documentation. The 'Local Simulator' node simulates a quantum computer using the local Qiskit library. It runs the quantum circuit and outputs the results.

Rules

1. Do not duplicate qubits
   To avoid inconsistencies, there should always be 1 instance of each qubit at all times. A node can take multiple qubits as input but only one wire should be connected to each output. To do so, always input as many qubits as the node outputs.

2. Wait for quantum circuit to execute
   Do not double-click the inject button, wait for the circuit to have finished executing before runnning it again.
   If such an issue occurs, please restart Node-RED.

Input nodes	Qubit nodes	Single qubit gate nodes	Multi qubits gate nodes	Output nodes

More information on 'quantum' nodes can be found in the Node-RED Quantum wiki.

Quantum Algorithm Nodes

Node-RED Quantum includes a 'quantum algorithm' library of nodes that can be used to leverage the power of quantum computing in classical programs.

The nodes do not require any specific quantum knowledge to be used, except for some initial knowledge on the algorithm itself to have a better understanding of its use.

Those nodes encapsulate all the quantum-related operations so that users just have to input the right data in order to receive the quantum algorithm output.

The 'quantum algorithm' library includes:

• Grover's searching algorithm
• Shor's factoring algorithm

More information on 'quantum algorithm' nodes can be found in the Node-RED Quantum wiki.

Contributing

For information on how to contribute, please read the CONTRIBUTING guidelines.

Acknowledgements

For details on the authors, please read the AUTHORS file.

This Node-RED library was developed in the context of a UCL IXN partnership with IBM. Defined and arranged by IBM, the project was allocated to students from UCL's Computer Science Department as part of their Master's thesis. Special thanks to John McNamara for overseeing the development of this project, to David Clark and Rae Harbird for their supervision as Academic Supervisors, and to Sieglinde Pfaendler and James Wootton for their advice and guidance as our Quantum Mentors.