node-red-contrib-msg-router 0.0.7

A Node Red node to route messages between nodes

npm install node-red-contrib-msg-router

node-red-contrib-msg-router

A Node Red node to route messages between nodes.

Introduction

This node makes a series of message routing types available in Node-Red, by sending the input messages to zero/one/multiple/all of its output ports:

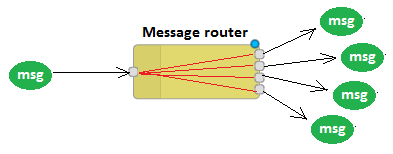
A series of different router types are available, to specify TO WHICH outputs the input message should be routed.

In most cases the Node-Red wires will be sufficient to send messages between nodes. For example when an output port is connected to 4 wires (i.e. to 4 input ports), the original input message will be send only through the first wire. Node-Red will create create a clone of the input message for every other wire:

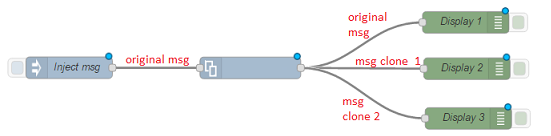
In some specific cases, this standard wiring behaviour might not be what you need. Nick pointed out here that he has some good reasons not changing this default behaviour. And in the near future the wiring mechanism in Node-Red will become pluggable, which means that other types of wiring might become available some day...

Some use cases for this node:

• Building a load balancer with a Node-Red flow. Remark: there might be better solutions available to accomplish the same result outside the Node-Red flow (e.g. MQTT, ...).
• Sending messages to multiple nodes without cloning them (for performance).
• Demultiplexer
• ...

Remark: this node functions similar to routers in Akka. Note that not all routers types from Akka have been implemented here, because in Node-Red the message router node doesn't get any feedback from the receiver nodes: this means the message router node is not aware of the load of the receiver nodes.

Install

Run the following npm command in your Node-RED user directory (typically ~/.node-red):

npm install node-red-contrib-msg-router

Usage

The node can be configured in a few steps, via the node's config screen:

• When a message needs to be routed to M receiver nodes, then start by adding M outputs.
• For each output a number of properties can be setup:
  • Active : When selected, the router will be able to send messages to that output. When deselected, the output will be ignored, and the messages will be distributed accross all other (active) outputs.
  • Clone: When selected, the router will clone every input message that will be send to this output.
  • Delay: When a value is specified (in milliseconds), each message send to this output will be delayed for the specified time period.
  • Weight: When a value is specified, the weight indicates the possibility that a message will be send to that output. The weight option will only be available for the 2 weighted router types. Weights can be used to setup outputs with different processing capacities. Outputs with higher weights receive more messages, compared to outputs with less weights.
• The specified router type will determine how the input messages are being routed to the N available outputs.

The msg.output field in the output message will be filled with the number of the output, to which the message has been routed. This field will be filled for all router types, except 'broadcast routing'. Reason is that for broadcasting, the same message might be send to all outputs (if cloning is disabled).

Router types

The router types specifies HOW the input messages will be routed to the M available outputs.

Broadcast routing

The broadcast router will send the input message to all active outputs. Since the same message is going to be send to multiple outputs, it is important to specify for each output following property:

• whether the original input message should be send.
• whether a clone of the input message should be send.

[{"id":"4bc0bb81.6627a4","type":"inject","z":"66fa353.41687cc","name":"Input msg","topic":"","payload":"Payload data","payloadType":"str","repeat":"","crontab":"","once":false,"x":171.00007247924805,"y":131.0000238418579,"wires":[["3606f2e1.8dd95e"]]},{"id":"3606f2e1.8dd95e","type":"msg-router","z":"66fa353.41687cc","routerType":"broadcast","topicDependent":false,"msgKeyField":"payload","outputsInfo":[{"active":true,"clone":false,"delay":"0","weight":"100"},{"active":true,"clone":false,"delay":"0","weight":"50"},{"active":true,"clone":false,"delay":"0","weight":"100"},{"active":true,"clone":false,"delay":"0","weight":"50"}],"name":"Router","delaying":"unrelated","msgControl":false,"outputs":"4","x":321.0000534057617,"y":131.66673278808594,"wires":[["d9a46560.65e3f8"],["d1661caa.2154d"],["1f9952d7.a3b82d"],["1176a62.aa0655a"]]},{"id":"d9a46560.65e3f8","type":"function","z":"66fa353.41687cc","name":"Counter1","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port1')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port1',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":489.503849029541,"y":45.796884536743164,"wires":[["c8ad5304.128b4"]]},{"id":"d1661caa.2154d","type":"function","z":"66fa353.41687cc","name":"Counter2","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port2')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port2',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":490.0001564025879,"y":101.99998664855957,"wires":[["56cfb8ca.c42e28"]]},{"id":"1176a62.aa0655a","type":"function","z":"66fa353.41687cc","name":"Counter4","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port4')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port4',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":491.0000648498535,"y":212.00006008148193,"wires":[["acbae15e.9083b"]]},{"id":"1f9952d7.a3b82d","type":"function","z":"66fa353.41687cc","name":"Counter3","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port3')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port3',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":489.0000801086426,"y":156.9999713897705,"wires":[["17a71165.cbf6ff"]]},{"id":"acbae15e.9083b","type":"debug","z":"66fa353.41687cc","name":"Output 4","active":true,"console":"false","complete":"payload","x":642.9998970031738,"y":211.99996852874756,"wires":[]},{"id":"17a71165.cbf6ff","type":"debug","z":"66fa353.41687cc","name":"Output 3","active":true,"console":"false","complete":"payload","x":641.9998970031738,"y":156.9999713897705,"wires":[]},{"id":"56cfb8ca.c42e28","type":"debug","z":"66fa353.41687cc","name":"Output 2","active":true,"console":"false","complete":"payload","x":640.9998970031738,"y":101.99997138977051,"wires":[]},{"id":"c8ad5304.128b4","type":"debug","z":"66fa353.41687cc","name":"Output 1","active":true,"console":"false","complete":"payload","x":641.9998970031738,"y":45.99997138977051,"wires":[]},{"id":"40899b5a.a61244","type":"comment","z":"66fa353.41687cc","name":"Broadcast routing","info":"","x":169.50007247924805,"y":50.79296398162842,"wires":[]}]

When the load should be distributed across time, a delay can be specified for each output. Otherwise the message will arrive at all ports at the same time:

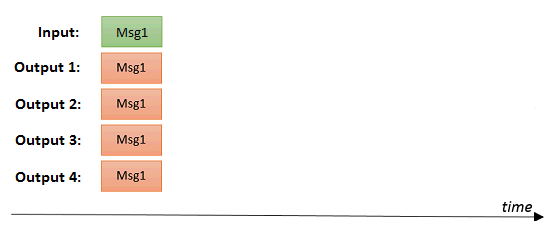
Remark: when the router type is 'broadcasting' combined with cloning for all outputs except the first one, the behaviour of this node will be identical to standard Node-Red wires.

Message based routing

The message based router will send the input message to the output, which is specified inside the message itself. Each message needs to have a msg.output field, which contains the output number (from 1 to N).

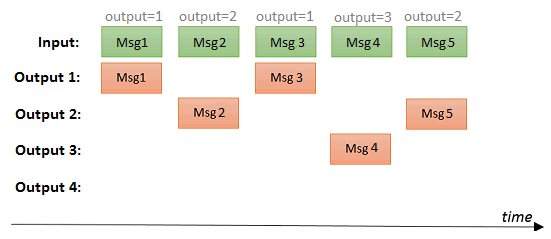
[{"id":"88f9acbf.63d1d","type":"inject","z":"66fa353.41687cc","name":"Input msg port 1","topic":"","payload":"1","payloadType":"num","repeat":"","crontab":"","once":false,"x":151.01987266540527,"y":593.0040001869202,"wires":[["79014416.6071fc"]]},{"id":"8f7bf8b2.d20898","type":"inject","z":"66fa353.41687cc","name":"Input msg port 2","topic":"","payload":"2","payloadType":"num","repeat":"","crontab":"","once":false,"x":151.01983451843262,"y":632.0039706230164,"wires":[["79014416.6071fc"]]},{"id":"2b31fa6d.0ec916","type":"inject","z":"66fa353.41687cc","name":"Input msg port 3","topic":"","payload":"3","payloadType":"num","repeat":"","crontab":"","once":false,"x":152.01986503601074,"y":670.0039553642273,"wires":[["79014416.6071fc"]]},{"id":"67a9cae3.8c09c4","type":"inject","z":"66fa353.41687cc","name":"Input msg port 4","topic":"","payload":"4","payloadType":"num","repeat":"","crontab":"","once":false,"x":151.01984214782715,"y":709.0039744377136,"wires":[["79014416.6071fc"]]},{"id":"79014416.6071fc","type":"change","z":"66fa353.41687cc","name":"set msg.output","rules":[{"t":"set","p":"output","pt":"msg","to":"payload","tot":"msg"}],"action":"","property":"","from":"","to":"","reg":false,"x":368.5119686126709,"y":648.8007578849792,"wires":[["ac395a68.284f28"]]},{"id":"9f61b61e.70ec68","type":"function","z":"66fa353.41687cc","name":"Counter1","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port1')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port1',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":735.5237197875977,"y":566.8008394241333,"wires":[["f91c8690.4fa098"]]},{"id":"cbcf3262.c889d","type":"function","z":"66fa353.41687cc","name":"Counter2","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port2')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port2',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":736.0200271606445,"y":623.0039415359497,"wires":[["6c4d28b3.093078"]]},{"id":"d0dcec11.a1a9a","type":"function","z":"66fa353.41687cc","name":"Counter4","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port4')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port4',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":737.0199356079102,"y":733.0040149688721,"wires":[["5daea0d9.31bbc"]]},{"id":"7fc2d97a.72e308","type":"function","z":"66fa353.41687cc","name":"Counter3","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port3')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port3',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":735.0199508666992,"y":678.0039262771606,"wires":[["14b975c5.83df3a"]]},{"id":"5daea0d9.31bbc","type":"debug","z":"66fa353.41687cc","name":"Output 4","active":true,"console":"false","complete":"payload","x":889.0197677612305,"y":733.0039234161377,"wires":[]},{"id":"14b975c5.83df3a","type":"debug","z":"66fa353.41687cc","name":"Output 3","active":true,"console":"false","complete":"payload","x":888.0197677612305,"y":678.0039262771606,"wires":[]},{"id":"6c4d28b3.093078","type":"debug","z":"66fa353.41687cc","name":"Output 2","active":true,"console":"false","complete":"payload","x":887.0197677612305,"y":623.0039262771606,"wires":[]},{"id":"f91c8690.4fa098","type":"debug","z":"66fa353.41687cc","name":"Output 1","active":true,"console":"false","complete":"payload","x":888.0197677612305,"y":567.0039262771606,"wires":[]},{"id":"76a7dc28.ec0f94","type":"comment","z":"66fa353.41687cc","name":"Message based routing","info":"","x":470.51981925964355,"y":577.796998500824,"wires":[]},{"id":"ac395a68.284f28","type":"msg-router","z":"66fa353.41687cc","routerType":"message","topicDependent":false,"msgKeyField":"payload","outputsInfo":[{"active":true,"clone":false,"delay":"0","weight":"0"},{"active":true,"clone":false,"delay":"0","weight":"0"},{"active":true,"clone":false,"delay":"0","weight":"0"},{"active":true,"clone":false,"delay":"0","weight":"0"}],"name":"","delaying":"unrelated","msgControl":false,"outputs":"4","x":537.5001888275146,"y":648.3333563804626,"wires":[["9f61b61e.70ec68"],["cbcf3262.c889d"],["7fc2d97a.72e308"],["d0dcec11.a1a9a"]]}]

Remark: this type of routing can e.g. be used to create some kind of ON/OFF switch:

[{"id":"26c4b738.5d94e8","type":"inject","z":"66fa353.41687cc","name":"Input msg","topic":"","payload":"Payload data","payloadType":"str","repeat":"","crontab":"","once":false,"x":357.0197982788086,"y":302.2072124481201,"wires":[["d3360ae.f15e8f8"]]},{"id":"d3360ae.f15e8f8","type":"msg-router","z":"66fa353.41687cc","routerType":"broadcast","topicDependent":false,"msgKeyField":"payload","outputsInfo":[{"active":true,"clone":false,"delay":"0","weight":"100"}],"name":" Router","delaying":"unrelated","msgControl":true,"outputs":"1","x":527.0198097229004,"y":301.8739700317383,"wires":[["7f64c325.dc6abc"]]},{"id":"7f64c325.dc6abc","type":"function","z":"66fa353.41687cc","name":"Counter1","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port1')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port1',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":677.5236434936523,"y":302.0040922164917,"wires":[["356d9cc.6548164"]]},{"id":"356d9cc.6548164","type":"debug","z":"66fa353.41687cc","name":"Output 1","active":true,"console":"false","complete":"payload","x":837.0197448730469,"y":302.2071762084961,"wires":[]},{"id":"626f8aba.b40f24","type":"comment","z":"66fa353.41687cc","name":"Simple on/off switch","info":"","x":141.51982498168945,"y":297.00018405914307,"wires":[]},{"id":"989c78b6.d504b8","type":"inject","z":"66fa353.41687cc","name":"Disable output","topic":"","payload":"false","payloadType":"bool","repeat":"","crontab":"","once":false,"x":141.01984786987305,"y":348.0041341781616,"wires":[["69a29b6f.2296a4"]]},{"id":"69a29b6f.2296a4","type":"change","z":"66fa353.41687cc","name":"","rules":[{"t":"set","p":"output","pt":"msg","to":"1","tot":"num"},{"t":"set","p":"active","pt":"msg","to":"payload","tot":"msg"}],"action":"","property":"","from":"","to":"","reg":false,"x":343.52370834350586,"y":347.79706859588623,"wires":[["d3360ae.f15e8f8"]]},{"id":"86696b6.57d0698","type":"inject","z":"66fa353.41687cc","name":"Enable output","topic":"","payload":"true","payloadType":"bool","repeat":"","crontab":"","once":false,"x":140.01982498168945,"y":389.00413846969604,"wires":[["69a29b6f.2296a4"]]}]

Random routing

The random router will send the input message to one randomly chosen output.

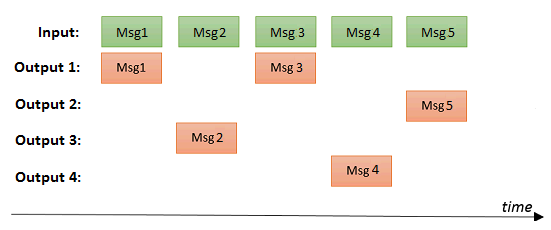
Weighted random routing (since version 0.0.2)

Same mechanism as a normal random routing, but the weighted random router allows each port to have a weight. A weight is an integer value that defines the processing capacity of that output: outputs with heigher weight will receive more messages (since they should have enough processing capacity), compared to outputs with less weight.

Round Robin routing

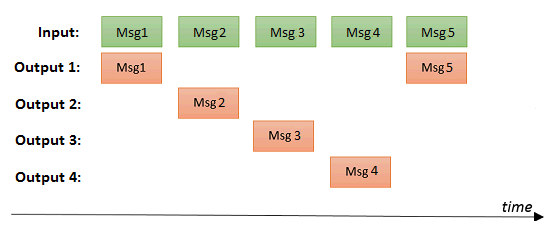
The Round Robin router will send the input message to the next output, in a sequential order. Suppose we have N outputs:

• The 1-st message will be send to output 1
• The 2-th message will be send to output 2
• ...
• The n-th message will be send to output N
• The (n+1)-th message will again be send to ouput 1
• ...

So as soon as all outputs have received a message, the cycle starts all over again at the first output ...

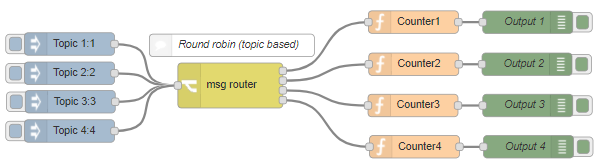
This router type can be setup as topic dependent, which means that each msg.topic will get its own sequence. For example the next message for topic A will be send to output 5, while the next message for topic B will be send to output 2:

[{"id":"62421ec.ca206e","type":"inject","z":"66fa353.41687cc","name":"","topic":"Topic 1","payload":"1","payloadType":"num","repeat":"","crontab":"","once":false,"x":434.00013732910156,"y":1592.000615119934,"wires":[["cf880f7e.f9673"]]},{"id":"680dfb4b.dfedf4","type":"inject","z":"66fa353.41687cc","name":"","topic":"Topic 2","payload":"2","payloadType":"num","repeat":"","crontab":"","once":false,"x":434.0000991821289,"y":1631.0005855560303,"wires":[["cf880f7e.f9673"]]},{"id":"56324ad9.de2d04","type":"inject","z":"66fa353.41687cc","name":"","topic":"Topic 3","payload":"3","payloadType":"num","repeat":"","crontab":"","once":false,"x":435.00012969970703,"y":1669.0005702972412,"wires":[["cf880f7e.f9673"]]},{"id":"8e424dc1.bdd12","type":"inject","z":"66fa353.41687cc","name":"","topic":"Topic 4","payload":"4","payloadType":"num","repeat":"","crontab":"","once":false,"x":434.00010681152344,"y":1708.0005893707275,"wires":[["cf880f7e.f9673"]]},{"id":"9a001969.a96088","type":"function","z":"66fa353.41687cc","name":"Counter1","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port1')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port1',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":892.5039138793945,"y":1562.7969274520874,"wires":[["9bf4e612.3d1f88"]]},{"id":"e36e1934.e79268","type":"function","z":"66fa353.41687cc","name":"Counter2","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port2')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port2',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":893.0002212524414,"y":1619.0000295639038,"wires":[["f3dea0f9.f2125"]]},{"id":"65e6e844.56de18","type":"function","z":"66fa353.41687cc","name":"Counter4","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port4')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port4',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":894.000129699707,"y":1729.0001029968262,"wires":[["efcdad3a.8b969"]]},{"id":"b097101b.8e1ea","type":"function","z":"66fa353.41687cc","name":"Counter3","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port3')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port3',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":892.0001449584961,"y":1674.0000143051147,"wires":[["5b1efe4b.80bcf"]]},{"id":"efcdad3a.8b969","type":"debug","z":"66fa353.41687cc","name":"Output 4","active":true,"console":"false","complete":"payload","x":1045.9999618530273,"y":1729.0000114440918,"wires":[]},{"id":"5b1efe4b.80bcf","type":"debug","z":"66fa353.41687cc","name":"Output 3","active":true,"console":"false","complete":"payload","x":1044.9999618530273,"y":1674.0000143051147,"wires":[]},{"id":"f3dea0f9.f2125","type":"debug","z":"66fa353.41687cc","name":"Output 2","active":true,"console":"false","complete":"payload","x":1043.9999618530273,"y":1619.0000143051147,"wires":[]},{"id":"9bf4e612.3d1f88","type":"debug","z":"66fa353.41687cc","name":"Output 1","active":true,"console":"false","complete":"payload","x":1044.9999618530273,"y":1563.0000143051147,"wires":[]},{"id":"b03f1072.c39eb","type":"comment","z":"66fa353.41687cc","name":"Round robin (topic based)","info":"","x":650.5,"y":1593.7932262420654,"wires":[]},{"id":"cf880f7e.f9673","type":"msg-router","z":"66fa353.41687cc","routerType":"roundrobin","topicDependent":true,"msgKeyField":"payload","outputsInfo":[{"active":true,"clone":false,"delay":"0","weight":"0"},{"active":true,"clone":false,"delay":"0","weight":"0"},{"active":true,"clone":false,"delay":"0","weight":"0"},{"active":true,"clone":false,"delay":"0","weight":"0"}],"name":"","delaying":"unrelated","msgControl":false,"outputs":"4","x":648.4803161621094,"y":1647.3293561935425,"wires":[["9a001969.a96088"],["e36e1934.e79268"],["b097101b.8e1ea"],["65e6e844.56de18"]]}]

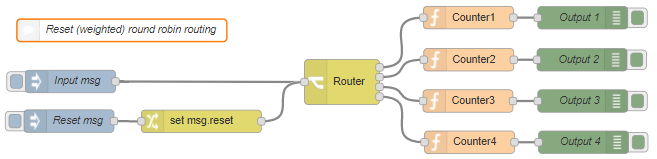
The Round Robin router can be reset (since version 0.0.2), by sending an input message with msg.reset set to true:

[{"id":"9d99ed1a.6a2f9","type":"inject","z":"66fa353.41687cc","name":"Input msg","topic":"","payload":"Payload data","payloadType":"str","repeat":"","crontab":"","once":false,"x":306,"y":2184.66650390625,"wires":[["5525ce45.51e24"]]},{"id":"5525ce45.51e24","type":"msg-router","z":"66fa353.41687cc","routerType":"weightedroundrobin","topicDependent":false,"counterReset":true,"msgKeyField":"payload","outputsInfo":[{"active":true,"clone":false,"delay":"0","weight":"100"},{"active":true,"clone":false,"delay":"0","weight":"100"},{"active":true,"clone":false,"delay":"0","weight":"100"},{"active":true,"clone":false,"delay":"0","weight":"100"}],"name":"Router                  ","delaying":"unrelated","msgControl":false,"outputs":"4","x":667.9999008178711,"y":2185.3330516815186,"wires":[["bf477df0.9bf7"],["7f7c73e1.f12d4c"],["20a9d419.e4f28c"],["551276e1.f586e8"]]},{"id":"bf477df0.9bf7","type":"function","z":"66fa353.41687cc","name":"Counter1","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port1')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port1',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":836.5036964416504,"y":2099.463203430176,"wires":[["c2b3ce65.098a8"]]},{"id":"7f7c73e1.f12d4c","type":"function","z":"66fa353.41687cc","name":"Counter2","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port2')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port2',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":837.0000038146973,"y":2155.666305541992,"wires":[["637e7f38.28623"]]},{"id":"551276e1.f586e8","type":"function","z":"66fa353.41687cc","name":"Counter4","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port4')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port4',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":837.9999122619629,"y":2265.6663789749146,"wires":[["22f29ed1.9b33f2"]]},{"id":"20a9d419.e4f28c","type":"function","z":"66fa353.41687cc","name":"Counter3","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port3')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port3',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":835.999927520752,"y":2210.666290283203,"wires":[["a92d84d1.7f0b28"]]},{"id":"22f29ed1.9b33f2","type":"debug","z":"66fa353.41687cc","name":"Output 4","active":true,"console":"false","complete":"payload","x":989.9997444152832,"y":2265.66628742218,"wires":[]},{"id":"a92d84d1.7f0b28","type":"debug","z":"66fa353.41687cc","name":"Output 3","active":true,"console":"false","complete":"payload","x":988.9997444152832,"y":2210.666290283203,"wires":[]},{"id":"637e7f38.28623","type":"debug","z":"66fa353.41687cc","name":"Output 2","active":true,"console":"false","complete":"payload","x":987.9997444152832,"y":2155.666290283203,"wires":[]},{"id":"c2b3ce65.098a8","type":"debug","z":"66fa353.41687cc","name":"Output 1","active":true,"console":"false","complete":"payload","x":988.9997444152832,"y":2099.666290283203,"wires":[]},{"id":"d30f233d.2073c","type":"comment","z":"66fa353.41687cc","name":"Reset (weighted) round robin routing","info":"","x":374.5,"y":2116.459517478943,"wires":[]},{"id":"b71eef56.33111","type":"inject","z":"66fa353.41687cc","name":"Reset msg","topic":"","payload":"Payload data","payloadType":"str","repeat":"","crontab":"","once":false,"x":304.0000343322754,"y":2237.463544845581,"wires":[["76a2c5b0.c4aa8c"]]},{"id":"76a2c5b0.c4aa8c","type":"change","z":"66fa353.41687cc","name":"","rules":[{"t":"set","p":"reset","pt":"msg","to":"true","tot":"bool"}],"action":"","property":"","from":"","to":"","reg":false,"x":480.49996185302734,"y":2237.796714782715,"wires":[["5525ce45.51e24"]]}]

The next message (after the reset message) with the same topic will be send to ouput 1, which means that the output counter has been reset. Make sure that the 'Allow counter reset using messages' checkbox is selected, otherwise the reset message will processed as a normal message.

Weighted Round Robin routing

Same mechanism as a normal Round Robin routing, but the weighted Round Robin router allows each port to have a weight. A weight is an integer value that defines the processing capacity of that output: outputs with heigher weight will receive more messages (since they should have enough processing capacity), compared to outputs with less weight.

When all weights have the same value, the router will behave like a standard (non-weighted) Round Robin router.

Watch out: weights with value 0 can result in issues, so it is adviced to disable such outputs instead.

A weighted Round Robin router can be reset and can be topic dependant: see the standard Round Robin router for more explanation about those both settings.

Consistent hashing routing

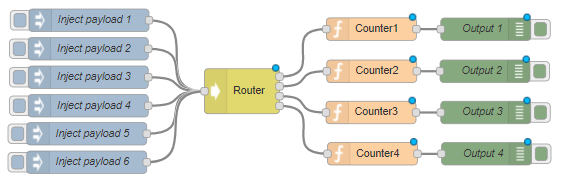
The consistent hashing router will send all input messages with the same value (hashed) to the same output port. Any field of the input message can be specified to contain the hash key. And any object can be used as a key, but usually a string or number or unique id (guid) will be used.

The key field needs to be specified, which is the field of the input message from which a hash value will be calculated. For example when all traffic of the same IP address should be forwarded to the same output, the key field could be msg.ip.

Starting from version 0.0.4:

• The key field can also contain nested message properties, for example msg.payload.device.ip.
• The router will ignore the input message (and show an error message) when the input message doesn't contain the required key field. However when the 'Allow messages with an undefined hash' checkbox is selected, all those messages (with hash value 'undefined') will be forwarded to the same output port.

[{"id":"a703a95.b7b4758","type":"inject","z":"66fa353.41687cc","name":"Inject payload 1","topic":"","payload":"Payload 1","payloadType":"str","repeat":"","crontab":"","once":false,"x":192.00021171569824,"y":825.6667900085449,"wires":[["16950053.d4ffe"]]},{"id":"16950053.d4ffe","type":"msg-router","z":"66fa353.41687cc","routerType":"hashing","topicDependent":false,"msgKeyField":"payload","outputsInfo":[{"active":true,"clone":false,"delay":"0","weight":"400"},{"active":true,"clone":false,"delay":"0","weight":"100"},{"active":true,"clone":false,"delay":"0","weight":"100"},{"active":true,"clone":false,"delay":"0","weight":"0"}],"name":" Router","delaying":"increment_active","msgControl":false,"outputs":"4","x":396.00022888183594,"y":920.3334274291992,"wires":[["8df51c96.6cd63"],["2b872f55.a46fe"],["ef9ceb78.a277e8"],["6536c470.c2fd4c"]]},{"id":"8df51c96.6cd63","type":"function","z":"66fa353.41687cc","name":"Counter1","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port1')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port1',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":568.5040292739868,"y":837.4635877609253,"wires":[["69344b0b.c1a0b4"]]},{"id":"2b872f55.a46fe","type":"function","z":"66fa353.41687cc","name":"Counter2","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port2')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port2',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":569.0003366470337,"y":893.6666898727417,"wires":[["4e2a3587.b3bc0c"]]},{"id":"6536c470.c2fd4c","type":"function","z":"66fa353.41687cc","name":"Counter4","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port4')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port4',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":570.0002450942993,"y":1003.6667633056641,"wires":[["304842b2.143abe"]]},{"id":"ef9ceb78.a277e8","type":"function","z":"66fa353.41687cc","name":"Counter3","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port3')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port3',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":568.0002603530884,"y":948.6666746139526,"wires":[["7a80a645.c84378"]]},{"id":"304842b2.143abe","type":"debug","z":"66fa353.41687cc","name":"Output 4","active":true,"console":"false","complete":"payload","x":722.0000772476196,"y":1003.6666717529297,"wires":[]},{"id":"7a80a645.c84378","type":"debug","z":"66fa353.41687cc","name":"Output 3","active":true,"console":"false","complete":"payload","x":721.0000772476196,"y":948.6666746139526,"wires":[]},{"id":"4e2a3587.b3bc0c","type":"debug","z":"66fa353.41687cc","name":"Output 2","active":true,"console":"false","complete":"payload","x":720.0000772476196,"y":893.6666746139526,"wires":[]},{"id":"69344b0b.c1a0b4","type":"debug","z":"66fa353.41687cc","name":"Output 1","active":true,"console":"false","complete":"payload","x":721.0000772476196,"y":837.6666746139526,"wires":[]},{"id":"febcfc3b.51b93","type":"comment","z":"66fa353.41687cc","name":"Hash based routing","info":"","x":389.50016689300537,"y":792.4597420692444,"wires":[]},{"id":"cf488ad5.2a9488","type":"inject","z":"66fa353.41687cc","name":"Inject payload 2","topic":"","payload":"Payload 2","payloadType":"str","repeat":"","crontab":"","once":false,"x":191.00021171569824,"y":863.6667900085449,"wires":[["16950053.d4ffe"]]},{"id":"6ac96d2a.61f414","type":"inject","z":"66fa353.41687cc","name":"Inject payload 3","topic":"","payload":"Payload 3","payloadType":"str","repeat":"","crontab":"","once":false,"x":191.00021171569824,"y":901.6667900085449,"wires":[["16950053.d4ffe"]]},{"id":"3d64e53b.b6c1ba","type":"inject","z":"66fa353.41687cc","name":"Inject payload 4","topic":"","payload":"Payload 4","payloadType":"str","repeat":"","crontab":"","once":false,"x":191.00021171569824,"y":939.6667900085449,"wires":[["16950053.d4ffe"]]},{"id":"ec54cc68.c67c7","type":"inject","z":"66fa353.41687cc","name":"Inject payload 5","topic":"","payload":"Payload 5","payloadType":"str","repeat":"","crontab":"","once":false,"x":189.00021934509277,"y":977.0001931190491,"wires":[["16950053.d4ffe"]]},{"id":"3a88862b.d4075a","type":"inject","z":"66fa353.41687cc","name":"Inject payload 6","topic":"","payload":"payload 6","payloadType":"str","repeat":"","crontab":"","once":false,"x":189.00021934509277,"y":1015.0001964569092,"wires":[["16950053.d4ffe"]]}]

This can be used to group similar (i.e. with same value for a specified msg field) messages by output

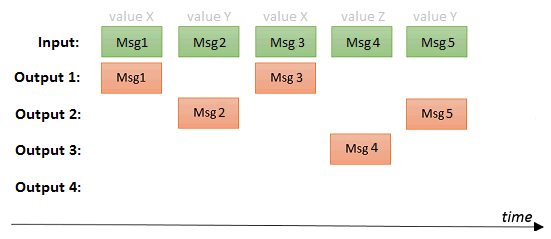
Remark: the router node decides on his own which value will be send to which port. If you want to specify this by yourself, you don't really need a router. Use in that case the standard Node-Red Switch node!

Weighted consistent hashing routing

Same mechanism as a normal consistent hashing routing, but the weighted consistent hashing router allows each port to have a weight. A weight is an integer value that defines the processing capacity of that output: outputs with heigher weight will receive more messages (since they should have enough processing capacity), compared to outputs with less weight.

Watch out: weights with value 0 can result in issues, so it is adviced to disable such outputs instead.

Cloning

Each port can be configured to retrieve the original input message, or a clone of it.

When an output port is connected to multiple input ports, the standard Node-Red wiring will send the original message to only 1 input. All the other inputs will get a clone of the message. That is a very obvious design design, to avoid multiple nodes manipulating the same message (which might result in strange behaviour).

However in some cases cloning should be avoided, especially when lot's of data is involved. For example when the messages contain images, unnecessary cloning of messages will result in bad performance. If the images are being send to N image manipulation nodes, cloning will be required. But when the images are being send to N image analyzing nodes (that don't manipulate the message content), it will be much faster to send the original message to those nodes.

CAUTION: Sending messages (without cloning) to multiple nodes might cause problems!!!

Delays

A delay can be specified (in milliseconds) for every output. These delays can be used by all router types. When a message arrives on an output, it will be delayed with the interval specified for that output.

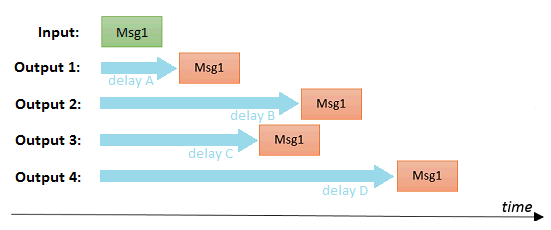
When N delay values have been specified, it is possible to apply relations between those separate values:

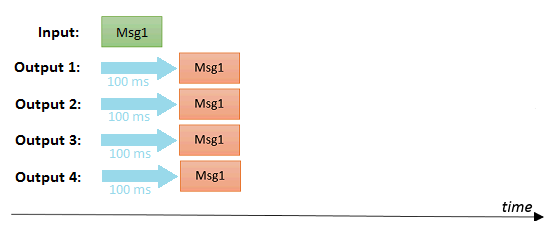
• The delay values can be unrelated to each other, which means each output get its own delay. E.g. when all 3 outputs for 'broadcasting' have a delay 100, they will all get a message after 100 ms.

  

• The delay values of all outputs can be incremented, which means that the delay of an output N is the sum of the delays of all outputs with a lower output number. E.g. when all 3 outputs have a delay 100, the message will be delayed 100 msec for output 1 and 200 msec for output 2 and 300 msec for output 3. The delay for output3 will stay 300 msec even when output 2 becomes inactive.

  

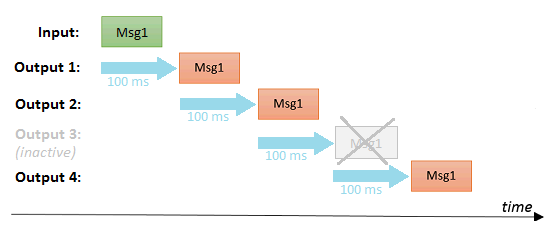
• The delay values of all active outputs can be incremented, which means that the delay of an output N is the sum of the delays of all active outputs with a lower output number. E.g. when all 3 outputs have a delay 100 (but output 2 is inactive), the message will be delayed 100 msec for output 1 and 200 msec for output 3.

  

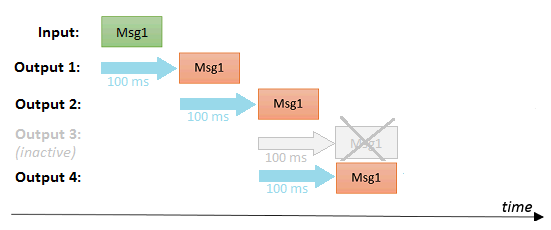
The advantage of 'unrelated' delays is that a lower output number can get its messages faster compared to a higher output number:

Output control via messages

When this option is enabled, the outputs can be configured using input messages. When an input message has a msg.output field, the same message can contain extra fields to configure that output:

• msg.active This field can override the 'Active' value of this output.
• msg.weight This field can override the 'Weight' value of this output.
• msg.clone This field can override the 'Clone' value of this output.
• msg.delay This field can override the 'Delay' value of this output (since version 0.0.2).

[{"id":"7a985c01.e0e0a4","type":"inject","z":"66fa353.41687cc","name":"Input msg","topic":"","payload":"Payload data","payloadType":"str","repeat":"","crontab":"","once":false,"x":308.00003814697266,"y":464.9999885559082,"wires":[["cab63b2e.8df848"]]},{"id":"cab63b2e.8df848","type":"msg-router","z":"66fa353.41687cc","routerType":"broadcast","topicDependent":false,"msgKeyField":"payload","outputsInfo":[{"active":true,"clone":false,"delay":"0","weight":"100"}],"name":" Router","delaying":"unrelated","msgControl":true,"outputs":"1","x":478.00004959106445,"y":464.66674613952637,"wires":[["8af9f9a7.56a9e8"]]},{"id":"8af9f9a7.56a9e8","type":"function","z":"66fa353.41687cc","name":"Counter1","func":"// initialise the counter to 0 if it doesn't exist already\nvar counter = flow.get('counter_port1')||0;\n\ncounter += 1;\n\n// store the value back\nflow.set('counter_port1',counter);\n\nnode.status({fill:\"green\",shape:\"dot\",text:\"count = \" + counter});\n\nreturn msg;","outputs":"1","noerr":0,"x":627.5038833618164,"y":464.7968683242798,"wires":[["bad0d226.0844"]]},{"id":"bad0d226.0844","type":"debug","z":"66fa353.41687cc","name":"Output 1","active":true,"console":"false","complete":"payload","x":787.9999847412109,"y":464.9999523162842,"wires":[]},{"id":"add096ed.c46f98","type":"inject","z":"66fa353.41687cc","name":"Configure","topic":"","payload":"false","payloadType":"bool","repeat":"","crontab":"","once":false,"x":132.00012588500977,"y":510.79698181152344,"wires":[["6cd61f8.46463e"]]},{"id":"6cd61f8.46463e","type":"change","z":"66fa353.41687cc","name":"Setup port 2","rules":[{"t":"set","p":"output","pt":"msg","to":"2","tot":"num"},{"t":"set","p":"clone","pt":"msg","to":"true","tot":"bool"},{"t":"set","p":"active","pt":"msg","to":"payload","tot":"msg"},{"t":"set","p":"weight","pt":"msg","to":"132","tot":"num"}],"action":"","property":"","from":"","to":"","reg":false,"x":296.5039482116699,"y":510.5898447036743,"wires":[["cab63b2e.8df848"]]},{"id":"62482c97.3e2964","type":"comment","z":"66fa353.41687cc","name":"Configuration","info":"","x":88,"y":460,"wires":[]}]

As soon as the message contains at least one of these 3 latter fields, the message is considered as a control message. Such messages are only used to configure an output, but are not routed to the outputs!

Notice that this updated configuration is not reflected in the node's config screen, since that screen contains the default configuration.